L2AW theorem
Local Reads and Linearizable Asynchronous Replication
L2AW theorem
Local Reads and Linearizable Asynchronous Replication
Ideally crash-tolerant replication protocols,
which are at the heart of read-intensive reliable datastores, must offer:
1) local reads (for performance),
2) linearizability (i.e., strong consistency), and
3) ensure safety under asynchrony.
However, existing crash-tolerant replication protocols provide up to two of the three above features:
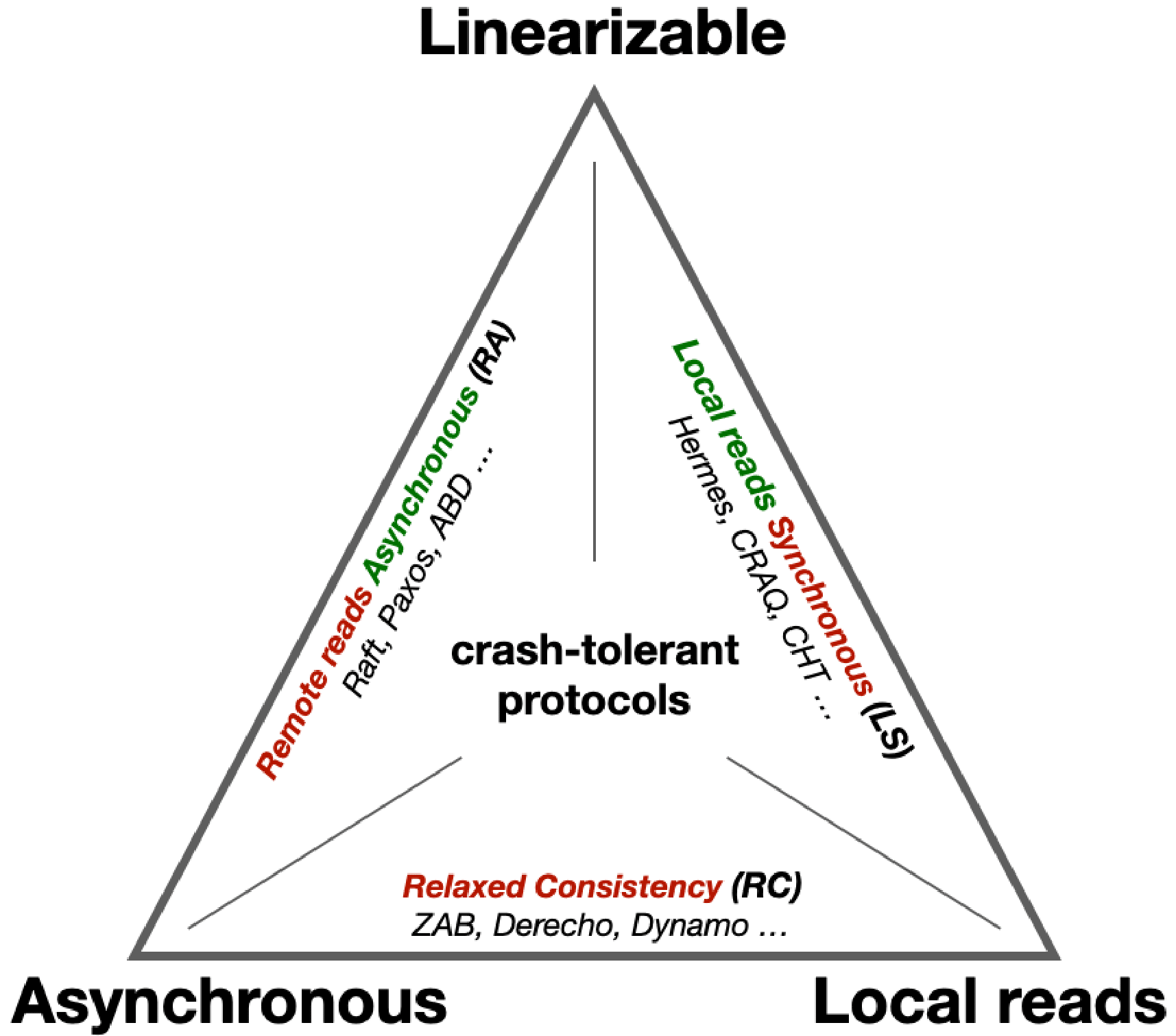
This hints a fundamental tradeoff between consistency, asynchrony, and performance in crash-tolerant
protocols.
Inspired by the above we introduce and prove the L2AW impossibility which asserts that: any
Linearizable Asynchronous read/write register protocol that tolerates a crash (Without
blocking reads or writes), has no Local reads.
Guided by the L2AW impossibility, we introduce the idea of almost-local reads (ALRs),
which can be implemented in a crash-tolerant and linearizable manner under asynchrony. ALRs inevitably have
higher latency than local (single-node) reads, but they are very lightweight, with computation and network
costs close to local reads.
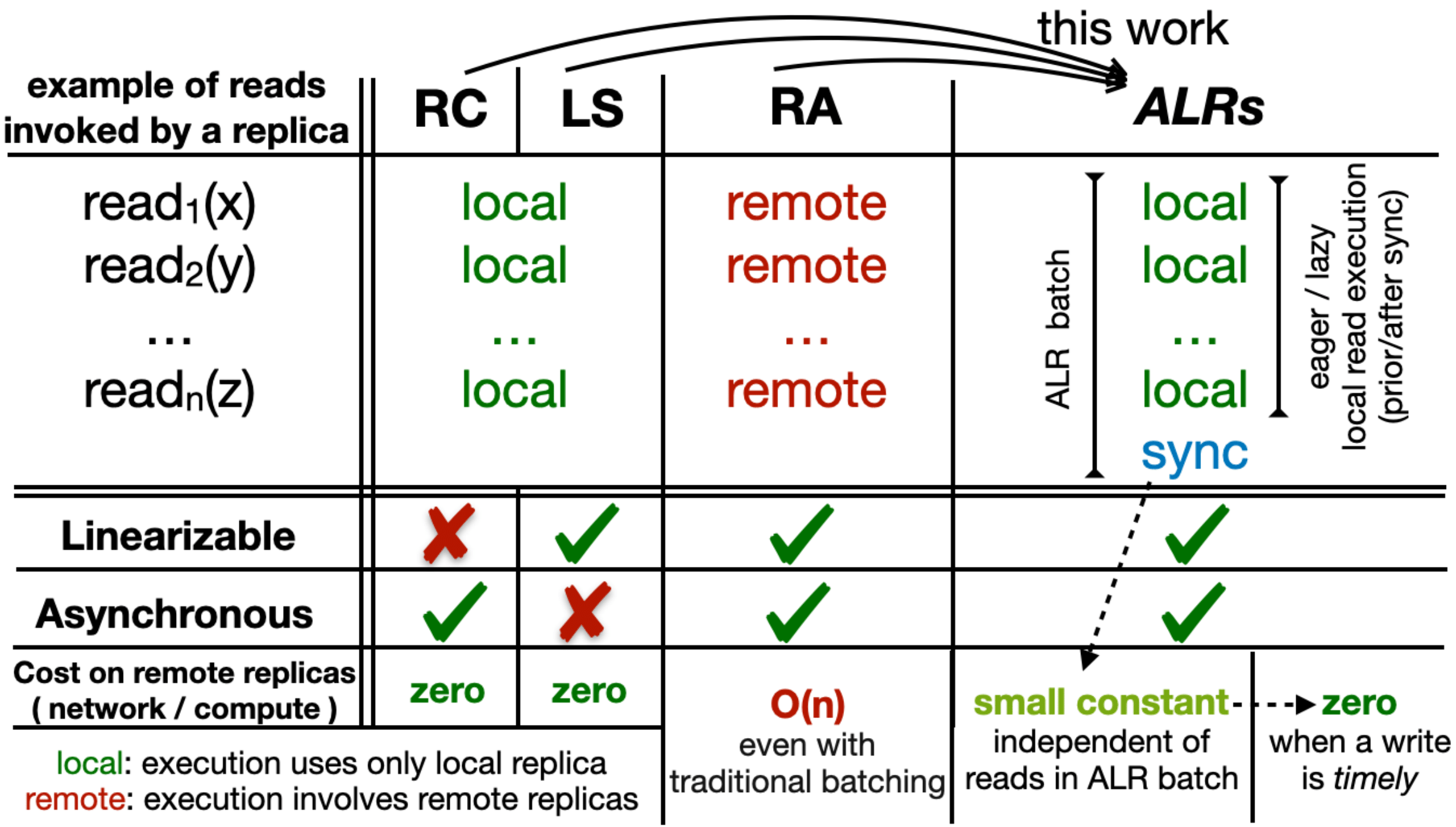
When applied to the protocols in all three corners of the
design space (i.e., RA, RC, LS), ALRs add the missing piece:
1) they improve the throughput for RA protocols
2) ensure linearizability for RC protocols and
3) allow LS protocols to safely operate under asynchrony.
HERMES: a
high-performance single-key fault-tolerant and strongly consistent replication protocol.
ZEUS:
locality-aware distributed (multi-key) transactions with high performance and reliability.
The code and accompanied materials are freely distributed to the public under the Apache 2.0 License.
If you have any questions regarding the L2AW theorem or ALRs do not hesitate to contact Antonis Katsarakis ( antonios.katsarakis {at} huawei.com ).